Mirley - Elektronika i Programowanie

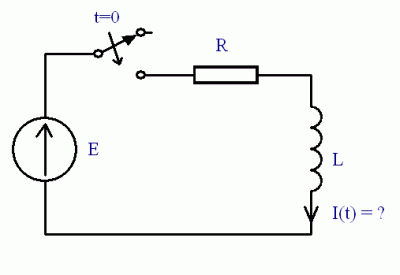
Metody zawarte tutaj są pomocne przy rozważaniu i analizie obwodów liniowych w których występują stany nieustalone, czyli stany przejściowe spowodowane obecnością w układzie elementów gromadzących energię (cewka, kondensator).

1. Warunki Początkowe - Prawa Komutacji

W cewce o indukcyjności $L$:

$$ U = L \frac{di}{dt}$$

Napięcie zależy od pochodnej prądu, więc nie może się on zmienić nagle, co oznacza że jeżeli w chwili $ t = 0 $ nastąpi odłączenie lub przyłączenie części obwodu to prąd płynący przez cewkę w chwili tuż przed przełączeniem $ i_L(0^-) $ będzie równy prądowi tuż po przełączeniu $ i_L(0^+) $. Zapisujemy to wzorem:

$$ i_L(0^-) = i_L(0) = i_L(0^+) $$

W kondensatorze o pojemności $C$ :

$$ I = C \frac{du}{dt}$$

Prąd zależy od pochodnej napięcia, więc nie może się ono zmienić nagle, co oznacza że jeżeli w chwili $ t = 0 $ nastąpi odłączenie lub przyłączenie części obwodu to napięcie na kondensatorze w chwili tuż przed przełączeniem $ u_C(0^-) $ będzie równe napięciu tuż po przełączeniu $ u_C(0^+) $. Zapisujemy to wzorem:

$$ u_C(0^-) = u_C(0) = u_C(0^+) $$

2. Klasyczne Metody Rozwiązywania (Równania Różniczkowe)

Klasyczne metody rozwiązywania obwodów z stanie nieustalonym polegają na rozwiązywaniu równań różniczkowych w celu znalezienia odpowiedzi czasowej obwodu. W układzie przedstawionym na rysunku poniżej zadaniem jest wyznaczyć wartość prądu $i_L(t)$. Począwszy od chwili $t=0$ w której wyłącznik zostaje zwarty:

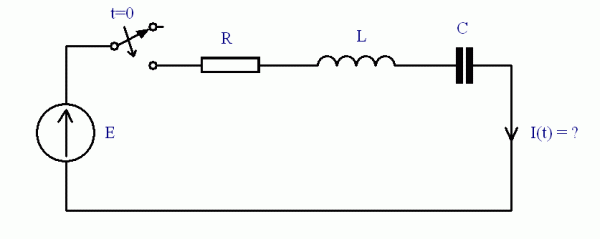
Przed komutacją (włączeniem przełącznika) prąd płynący przez cewkę był równy 0 a zatem:

$$ i_L(0^-) = 0 = i_L(0^+) $$

Zapisujemy równanie dla oczka obwodu:

$$ E = i_L R + L \frac{di_L}{dt} $$

Następnie rozwiązujemy otrzymując kolejno:

$$ E - i_L R = L \frac{di_L}{dt} $$

$$ \frac{dt}{L} = \frac{di_L}{E - i_L R} $$

Całkujemy stronami:

$$ \frac{t}{L} = ln(E - i_L R) \cdot \left(- \frac{1}{R} \right) + C_1 $$

$$ -t \frac{R}{L} = ln(E - i_L R) + C_2 $$

$$ E - i_L R = C \cdot e^{-t \frac{R}{L}} $$

$$ i_L = \frac{E}{R} - \frac{C}{R} \cdot e^{-t \frac{R}{L}} $$

Korzystamy z warunków początkowych i wyznaczamy stałą $ C $. W chwili $ t=0 $ prąd $ i_L = 0 $ a zatem:

$$ 0 = \frac{E}{R} - \frac{C}{R} $$

$$ C = E $$

Ostatecznym wynikiem jest:

$$ i_L = \frac{E}{R} - \frac{E}{R} \cdot e^{-t \frac{R}{L}} = \frac{E}{R} \cdot \left( 1 - e^{-t \frac{R}{L}} \right) $$

Pierwszy składnik postaci $ \frac{E}{R} $ nazywamy składową ustaloną, natomiast $ \frac{E}{R} \cdot e^{-t \frac{R}{L}} $ nazywamy składową nieustaloną.

3. Transformata Laplace'a

Transformata Laplace'a jest przekształceniem pewnej funkcji $ f(t) $ na funkcję $ F(s) $ zmiennej zespolonej $ s = \alpha + j \beta $:

$$ f(t) \rightarrow F(s) $$

Funkcja $ F(s) $ wyraża się wzorem:

$$ F(s) = \int_0^\infty f(t) \ e^{-st} dt $$

przy czym funkcja $ f(t) $ powinna być ciągła i jednoznaczna, a ponadto $ f(t) = 0$ dla $ t <0 $.

Symbolem transformaty jest $\mathcal{L}$

$$ F(s) = \mathcal{L}[f(t)]$$

Transformatą odwrotną nazywamy przekształcenie funkcji $ F(s) $ na funkcję $ f(t) $:

$$ F(s) \rightarrow f(t) $$

Ogólnie zapisujemy to wzorem:

$$ f(t) = \int_{c - j\infty}^{c + j\infty} F(s) \ e^{st} ds $$

Jeżeli funkcja $ F(s) $ jest postaci wymiernej:

$$ F(s) = \frac{P(s)}{Q(s)}$$

oraz stopień $ Q(s) $ jest wyższy niż $ P(s) $ to możemy wyrazić funkcję $ f(t) $ jako sumę residuów funkcji $ F(s) e^{st}$ po wszystkich pierwiastkach jej mianownika (po pierwiastkach $ Q(s) $)

$$ f(t) = \sum_{s=s_k} res[F(s) \ e^{st}] $$

Residuum wyrażamy wzorem:

$$ res[F(s) \ e^{st}]_{s_k} = \frac{1}{(l_k - 1)!} \quad \lim_{s \to s_k} \left[ \frac{d^{l_k -1}}{ds^{l_k - 1}} \left[(s - s_k)^{l_k} F(s) \ e^{st} \right] \right]$

gdzie $ l_k $ jest krotnością bieguna $ s_k $. Biegunami nazywamy pierwiastki mianownika funkcji $ F(s) $ czyli pierwiastki $ Q(s) $. Zerami nazywamy pierwiastki licznika funkcji $ F(s) $, czyli pierwiastki $ P(s) $.

Gdy biegun jest jednokrotny ($ l_k = 1 $) to wzór na residuum upraszcza się do postaci:

$$ res[F(s) \ e^{st}]_{s_k} = \lim_{s \to s_k} \left[(s - s_k) \ F(s) e^{st} \right] $$

Symbolem transformaty odwrotnej jest $\mathcal{L}^{-1}$

$$ f(t) = \mathcal{L}^{-1}[F(s)]$$

Własności transformaty Laplace'a:

$$ \mathcal{L}[\alpha f(t) + \beta g(t)] = \alpha \mathcal{L}[f(t)] + \beta \mathcal{L}[g(t)] = \alpha F(s) + \beta G(s)$$

$$ \mathcal{L}[f'(t)] = s F(s) - f(0^+)$$

$$\mathcal{L} \left[\int_0^t f(\tau) d \tau \right] = \frac{F(s)}{s}$$

$$\mathcal{L}[f(t - t_0)] = F(s) \ e^{-st_0}$$

$$\mathcal{L}[f(t) \ e^{-\lambda t}] = F(s + \lambda)$$

Jako przykład zastosowania transformaty rozważmy równanie różniczkowe zapisane dla oczka obwodu z początku tego artykułu:

$$ E = i R + L \frac{di}{dt} $$

mnożymy obustronnie równanie przez $ e^{-st} $ i całkujemy w granicach od 0 do $ \infty $ otrzymując:

$$ \int_0^\infty E e^{-st} dt = \int_0^\infty iR e^{-st} dt + \int_0^\infty L \frac{di}{dt} e^{-st} dt $$

Ostatni składnik całkujemy przez części:

$$ \int_0^\infty E e^{-st} dt = \int_0^\infty iR e^{-st} dt + L[i e^{-st}]_0^\infty + L \int_0^\infty i s e^{-st} dt $$

Wykorzystując poniższy wzór:

$$ F(s) = \int_0^\infty f(t) \ e^{-st} dt $$

zapisujemy równanie w prostej i zwartej postaci:

$$ E(s) = R i(s) - Li(0^+) + Ls i(s) $$

co po przekształceniu daje:

$$ \color{red} i(s) = \frac{E(s) + Li(0^+)}{R + sL}$$

Korzystamy z metody residuów, pamiętając że $ E(s) = \frac{E}{s} $ (ze względu na fakt że jest to skok jednostkowy pomnożony przez E) oraz uwzględniając warunki początkowe, szukamy rozwiązania w dziedzinie czasu. Zapisujemy zależność $ i(s) $:

$$ i(s) = \frac{E}{s(s +\frac{R}{L}) L } $$

$$ i(t) = res[i(s) \ e^{st}]_{0} + res[i(s) \ e^{st}]_{-\frac{R}{L}}$$

$$ i(t) = \lim_{s \to 0} \left[(s - 0) \frac{E \ e^{st}}{s(s +\frac{R}{L}) L} \right] + \lim_{s \to -\frac{R}{L}} \left[(s + \frac{R}{L}) \frac{E \ e^{st}}{s(s +\frac{R}{L}) L} \right] = \frac{E}{L} \frac{L}{R} e^0 + \frac{E}{L} \left( -\frac{L}{R} \right) e^{-t \frac{R}{L}} = \frac{E}{R} \left( 1- e^{-t \frac{R}{L}}\right)$$

Sposób rozwiązywania za pomocą transformaty Laplace'a może wydawać się dłuższy i bardziej skomplikowany, jednak w praktyce nie jest konieczne zapisywanie równań różniczkowych dla obwodu a następnie transformowanie ich do postaci operatorowej. Możemy od razu zapisać równania w postaci operatorowej a po wyliczeniu przetransformować do postaci zależnej od czasu za pomocą tabeli transformat (nie ma konieczności liczenia residuum)

4. Elementy RLC

W calu łatwiejszego zapisu równań posługujemy się gotowymi wzorami na wartość prądu i spadek napięcia na elementach RLC w stanie nieustalonym:

a) Rezystor

W dziedzinie czasu mamy:

$$ u(t) = R i(t) $$

Po transformacji:

$$ u(s) = R i(s) $$

b) Cewka

W dziedzinie czasu mamy:

$$ u(t) = L \frac{d i(t)}{dt} $$

Po transformacji:

$$ u(s) = Ls i(s) - L i(0^+)$$

$$ i(s) = \frac{u(s)}{sL} + \frac{i(0^+)}{s} $$

Impedancja cewki jest równa:

$$Z_L = sL$$

c) Kondensator

W dziedzinie czasu mamy:

$$ i(t) = C \frac{d u(t)}{dt} $$

Po transformacji:

$$ i(s) = Cs u(s) - C u(0^+)$$

$$ u(s) = \frac{i(s)}{sC} + \frac{u(0^+)}{s} $$

Impedancja kondensatora jest równa:

$$Z_C = \frac{1}{sC}$$

5. Operatorowe Metody Rozwiązywania (Laplace'a)

Operatorowe metody rozwiązywania obwodów w stanie nieustalonym polegają na zapisaniu równań w postaci operatowowej a następnie przedstawienie uzyskanego wyniku w dziedzinie czasu. W układzie przedstawionym na rysunku poniżej zadaniem jest wyznaczyć wartość prądu $i(t)$. Począwszy od chwili $t=0$ w której wyłącznik zostaje zwarty:

Na początku analizujemy obwód w stanie ustalonym określając napięcie stałe panujące na kondensatorze i prąd płynący przez cewkę przy rozwartym wyłączniku. A zatem:

$$u_C(0^-) = u_C(0^+) = 0$$

$$i_L(0^-) = i_L(0^+) = 0$$

Zapisujemy równanie dla oczka obwodu w postaci operatorowej (korzystamy z faktu że $ E(s) = \frac{E}{s} $):

$$\frac{E}{s} = i(s) \left( R +sL + \frac{1}{sC} \right)$$

po przekształceniu:

$$i(s) = \frac{\frac{E}{s}}{R +sL + \frac{1}{sC}}$$

$$i(s) = \frac{E}{L} \ \frac{1}{s^2 + \frac{Rs}{L} + \frac{1}{LC}}$$

$ \Delta = \left( \frac{R}{L} \right )^2 - \frac{4}{LC}$

Pierwiastkami mianownika są zatem:

$$ s_1 = -\frac{R}{2L} \ + \ \sqrt{\left( \frac{R}{2L} \right)^2 - \frac{1}{LC}} $$

$$ s_2 = -\frac{R}{2L} \ - \ \sqrt{\left( \frac{R}{2L} \right)^2 - \frac{1}{LC}} $$

Prąd $ i(s) $ przedstawiamy w ogólnej postaci:

$$ i(s) = \frac{E}{L} \ \frac{1}{(s-s_1)(s-s_2)} $$

Rozważymy teraz przypadki w zależności od $ \Delta $:

1. $ \Delta > 0$

Dla tego przypadku spełniona jest zależność: $ R \ > \ 2 \sqrt{\frac{L}{C}} $

$$ i(t) = res[i(s) \ e^{st}]_{s_1} + res[i(s) \ e^{st}]_{s_2} = \lim_{s \to s_1} \left[(s - s_1) \ \frac{E}{L} \ \frac{e^{st}}{(s - s_1)(s - s_2)} \right] + \lim_{s \to s_2} \left[(s - s_2) \ \frac{E}{L} \ \frac{e^{st}}{(s - s_1)(s - s_2)} \right] $$

$$ i(t) = \frac{E}{L} \ \frac{1}{s_1 - s_2} \ \left[ e^{s_1 t} - e^{s_2 t} \right] $$

po wstawieniu $ s_1 $ i $ s_2 $ otrzymamy:

$$ i(t) = \frac{E}{L} \ \frac{1}{2 \sqrt{\left( \frac{R}{2L} \right)^2 - \frac{1}{LC}}} \ \left[ \exp \left( -\frac{R}{2L} \ t \ + \ \sqrt{\left( \frac{R}{2L} \right)^2 - \frac{1}{LC}} \ t \right) \ - \ \exp \left(-\frac{R}{2L} \ t \ - \ \sqrt{\left( \frac{R}{2L} \right)^2 - \frac{1}{LC}} \ t \right) \right] $$

$$ i(t) = \frac{E}{L} \ \frac{1}{2 \sqrt{\left( \frac{R}{2L} \right)^2 - \frac{1}{LC}}} \ \exp \left( -\frac{R}{2L} \ t \right) \cdot \left[ \exp \left(\sqrt{\left( \frac{R}{2L} \right)^2 - \frac{1}{LC}} \ t \right) \ - \ \exp \left(- \sqrt{\left( \frac{R}{2L} \right)^2 - \frac{1}{LC}} \ t \right) \right] $$

Ostatecznie uzyskujemy zwartą postać:

$$ i(t) = \frac{E}{L} \ \frac{1}{\sqrt{\left( \frac{R}{2L} \right)^2 - \frac{1}{LC}}} \ \exp \left( -\frac{R}{2L} \ t \right) \cdot \sinh \left( \sqrt{\left( \frac{R}{2L} \right)^2 - \frac{1}{LC}} \ t \right) $$

2. $ \Delta = 0$

Dla tego przypadku spełniona jest zależność: $ R \ = \ 2 \sqrt{\frac{L}{C}} $

Mamy jeden podwójny pierwiastek: $ s_1 = s_2 = s_{12} = - \frac{R}{2L}$

$$ i(t) = res[i(s) \ e^{st}]_{s_{12}} = \frac{1}{(2 - 1)!} \ \lim_{s \to s_{12}} \left[ \frac{d^{2-1}}{ds^{2-1}} \left( (s - s_{12})^2 \ \frac{E}{L} \ \frac{e^{st}}{(s - s_{12})^2} \right) \right] $$

Po przekształceniu i podstawieniu otrzymujemy:

$$ i(t) = \lim_{s \to s_{12}} \left[ \frac{E}{L} \ t \cdot e^{st} \right] $$

$$ i(t) = \frac{E}{L} \ t \cdot e^{-\frac{R}{2L} \ t} $$

3. $ \Delta < 0$

Dla tego przypadku spełniona jest zależność: $ R \ < \ 2 \sqrt{\frac{L}{C}} $

Pierwiastkami są:

$$ s_1 = -\frac{R}{2L} \ + \ j \sqrt{\frac{1}{LC} - \left( \frac{R}{2L} \right)^2} $$

$$ s_2 = -\frac{R}{2L} \ - \ j \sqrt{\frac{1}{LC} - \left( \frac{R}{2L} \right)^2} $$

korzystamy z wyprowadzonej wcześniej zależności:

$$ i(t) = \frac{E}{L} \ \frac{1}{s_1 - s_2} \ \left[ e^{s_1 t} - e^{s_2 t} \right] $$

$$ i(t) = \frac{E}{L} \ \frac{1}{2j \sqrt{\frac{1}{LC} - \left( \frac{R}{2L} \right)^2}} \ \exp \left( -\frac{R}{2L} \ t \right) \cdot \left[ \exp \left( j \sqrt{ \frac{1}{LC} - \left( \frac{R}{2L} \right)^2} \ t \right) \ - \ \exp \left( -j \sqrt{\frac{1}{LC} - \left( \frac{R}{2L} \right)^2} \ t \right) \right] $$

Ostatecznie uzyskujemy zwartą postać:

$$ i(t) = \frac{E}{L} \ \frac{1}{\sqrt{\frac{1}{LC} - \left( \frac{R}{2L} \right)^2}} \ \exp \left( -\frac{R}{2L} \ t \right) \cdot \sin \left( \sqrt{ \frac{1}{LC} - \left( \frac{R}{2L} \right)^2} \ t \right) $$

6. Tabela Transformat